
Coordinate geometry and proof professional#
Tutors, instructors, experts, educators, and other professionals on the platform are independent contractors, who use their own styles, methods, and materials and create their own lesson plans based upon their experience, professional judgment, and the learners with whom they engage. Varsity Tutors connects learners with a variety of experts and professionals. Varsity Tutors does not have affiliation with universities mentioned on its website. Media outlet trademarks are owned by the respective media outlets and are not affiliated with Varsity Tutors.Īward-Winning claim based on CBS Local and Houston Press awards. Names of standardized tests are owned by the trademark holders and are not affiliated with Varsity Tutors LLC.Ĥ.9/5.0 Satisfaction Rating based upon cumulative historical session ratings through 12/31/20.
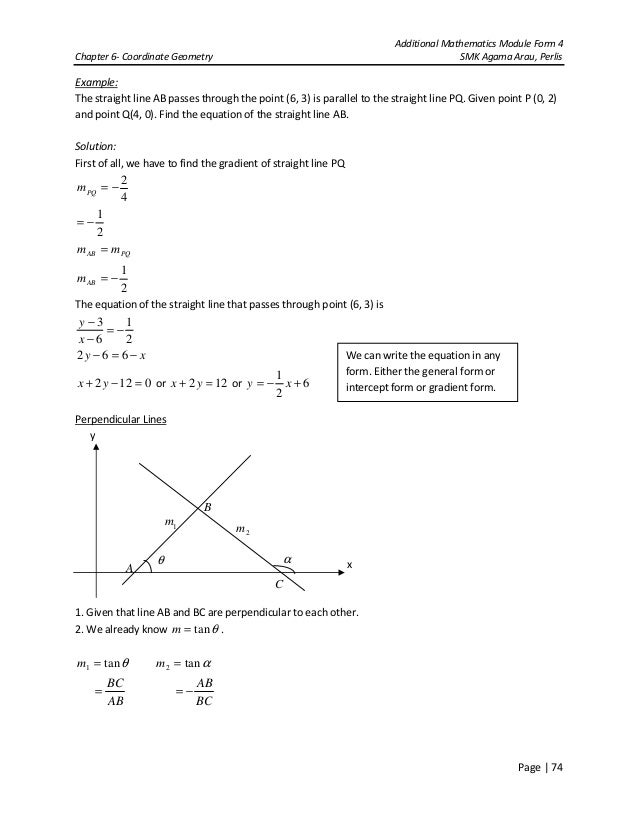
Now, compare the lengths of the two segments. (If it doesn't, you can just reflect the triangle over the We can assume without loss of generality that this third vertex lies in the first quadrant. Let the third vertex have the coordinates

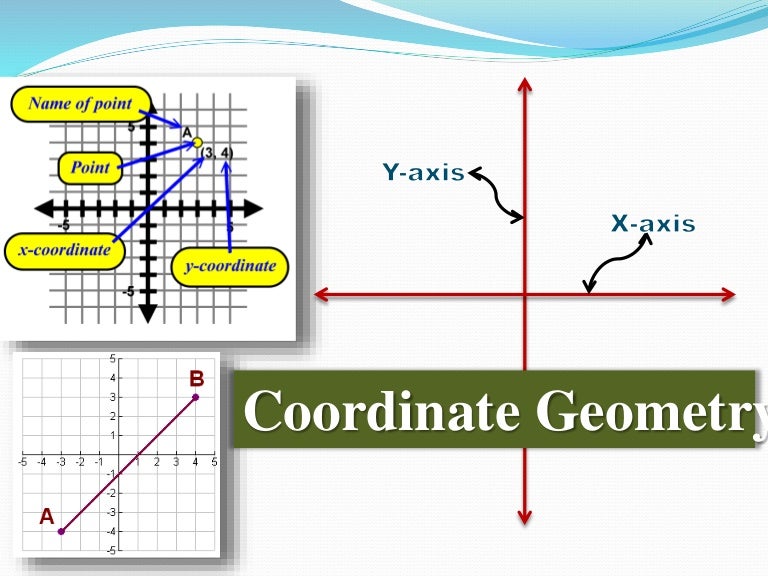
Without loss of generality, we can assume that one side of the triangle lies on the , which states that the segment connecting the midpoints of two sides of a triangle is parallel to the third side and exactly half the length. The method usually involves assigning variables to the coordinates of one or more points, and then using these variables in the midpoint orįor example, the following is a coordinate proof of the Is a proof of a geometric theorem which uses "generalized" points on the Cartesian Plane to make an argument.


 0 kommentar(er)
0 kommentar(er)
